Circle Theorems on Arcs

A part of the circumference of a circle is called an arc. In the figure, ACB is a part of the circumference of the circle with centre O. So, ACB is called an arc.

There are two types of arcs: minor arc and major arc. A minor arc is less than the half of the circumference and a major arc is greater than the half of the circumference.

 

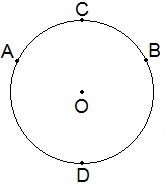
So, arc ACB is a minor arc and arc ADB is a major arc. 

THEOREM 4:

“Arcs subtended by equal angles at the centre of the circle are equal.”

This theorem can be verified by an experiment. Here is the experimental verification of the theorem:

 

Experimental Verification:

 

Construction: By using a pencil and compass, two circles of different radii with centre at ‘O’ are drawn. In each figure, with the help of a protractor two equal angles POQ and ROS at the centre are drawn.

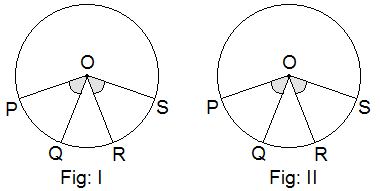
With the help of a thread, arcs PQ and RS of each figure are measured and the results are tabulated below:

Table:

 

Conclusion: The above experiment shows that arcs subtended by equal angles at the centre of the circle are equal.

 

 

CONVERSE OF THEOREM 4: 

“Angles subtended by two equal arcs of a circle at the centre are equal.”

 

This converse theorem also can be verified by an experiment. Here is the experimental verification of the theorem:

 

Experimental Verification:

 

Construction: By using a pencil and compass, two circles of different radii with centre at ‘O’ are drawn. With the help of compass two equal arcs XY and MN in each figure are drawn. Points X, Y, M, and N are joined with the centre O.

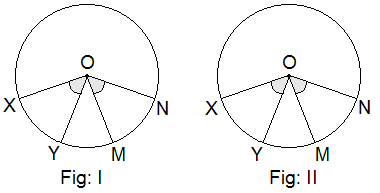
With the help of a protractor, central angles XOY and MON of each figure are measured and the results are tabulated below:

 

Table:

  

Conclusion: The above experiment shows that the angles subtended by equal arcs at the centre of the circle are equal.

 

 

THEOREM 5:

“Arcs cut off by equal chords of a circle are equal. Or, If two chords of a circle are equal, the corresponding arcs are equal.”

 

This theorem can be verified by an experiment. Here is the experimental verification of the theorem:

 

Experimental Verification:

 

Construction: By using a compass and pencil, two circles of different radii with centre O are drawn. In each figure, two equal chords JK and MN are drawn.

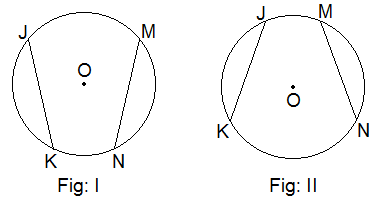
With the help of a thread, arcs JK and MN are measured in each circle and the results are tabulated below:

 

Table:

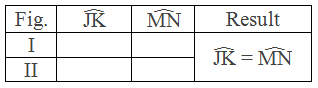
Conclusion: The above experiment shows that if two chords of a circle are equal, the corresponding arcs are equal.

 

 

CONVERSE OF THEOREM 5:

“If two arcs of a circle are equal, the corresponding chords are equal.”

 

This theorem can be verified by an experiment. Here is the experimental verification of the theorem:

 

Experimental Verification:

 

Construction: By using a compass and pencil, two circles of different radii with centre O are drawn. In each figure, arc AB = arc CD are also drawn. Then the chords AB and CD are drawn.

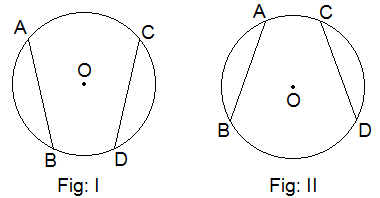
With the help of a divider and a scale, chords AB and CD are measured and the results are tabulated below:

 

Table:

 

Conclusion: The above experiment shows that if two arcs of a circle are equal, the corresponding chords are equal.

 

 

THEOREM 6:

“The angle at the centre of a circle is double the angle at the circumference standing on the same arc.”

 

This theorem can be verified experimentally as well as theoretically.

 

Experimental Verification:

 

Construction: By using a compass and pencil, two circles of different radii with centre O are drawn. In each figure, ∠AOB at the centre and ∠ACB at the circumference standing on the same arc AB are drawn.

With the help of a protractor, ∠AOB and ∠ACB of each figure are measured and the results are tabulated below:

 

Table:

 

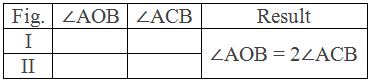
Conclusion: The above experiment shows that the angle at the centre of a circle is double the angle at the circumference standing on the same arc.

 

Theoretical Proof:

 

Given: O is the centre of the circle. Central angle ∠AOB and the circumference angle ∠ACB are standing on the same arc ADB.

To Prove: ∠AOB = 2∠ACB

 

Proof:

Statements                       Reasons

1.  ∠AOB = arc ADB ----> Central angle is equal to the opposite arc.

2.  ∠ACB = ½ arc ADB ----> Circumference angle is half of opposite arc.

Or, 2∠ACB = arc ADB

3.  ∠AOB = 2∠ACB -----> From statements 1 and 2.

Proved.

 

 

THEOREM 7:

“The angle in a semi-circle is a right angle.”

 

This theorem can be verified experimentally as well as theoretically.

 

Experimental Verification:

 

Construction: By using a compass and pencil, two circles of different radii with centre O are drawn. In each figure, diameter AB and ∠ACB are drawn.

 

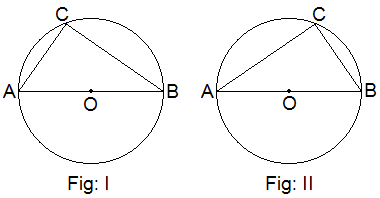
With the help of a protractor, ∠ACB of each figure is measured and the results are tabulated below:

 

Table:

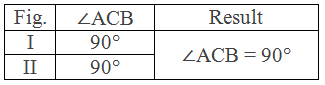
Conclusion: The above experiment shows that the angle in a semi-circle is a right angle.

 

Theoretical Proof:

 

Given: ACB is an angle in the semi-circle with centre at O and diameter AB.

To Prove: ∠ACB = 90°

 

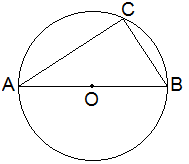
Proof:

Statements                       Reasons

4.  ∠ACB = ½ ∠AOB ----> Circumference angle is half of central angle.

5.  ∠AOB = 180° ----> Circumference angle is half of opposite arc.

6.  ∠ACB = ½ × 180° -----> From statements 1 and 2.

Or, ∠ACB = 90°

Proved. 

 

 

THEOREM 8:

“The angles at the circumference of a circle standing on the same arc are equal. OR, Angles in the same segment of a circle are equal.”

 

This theorem can be verified experimentally as well as theoretically.

 

Experimental Verification:

 

Construction: By using a compass and pencil, two circles of different radii with centre O are drawn. In each figure, circumference angles ∠ACB and ∠ADB standing on the same arc AB are drawn.

 

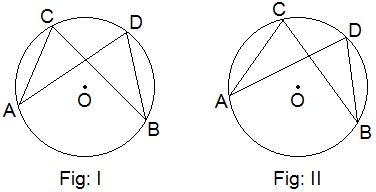
With the help of a protractor, ∠ACB and ∠ADB of each figure are measured and the results are tabulated below:

 

Table:

 

Conclusion: The above experiment shows that the circumference angles standing on the same arc or segment are equal.

 

Theoretical Proof:

 

Given: O is the centre of the circle. ∠ACD and ∠ABD are inscribed angles on the same arc AD.

To Prove: ∠ACB = ∠ABD

Construction: A and D are joined with O.

Proof:

Statements                       Reasons

1.     ∠ACD = ½ ∠AOD -----> Inscribed angle is half of central angle.

2.  ∠ABD = ½ ∠AOD -----> Inscribed angle is half of central angle.

3.  ∠ACD = ∠ABD -----> From statements 1 and 2.

Proved.

 

 

THEOREM 9:

“The opposite angles of a cyclic quadrilateral are supplementary. OR, Angles in opposite segments of a circle are supplementary.”

 

This theorem can be verified experimentally as well as theoretically.

 

Experimental Verification:

 

Construction: By using a compass, scale and pencil, two circles of different radii with centre O are drawn. In each figure, cyclic quadrilateral ABCD are drawn.

 

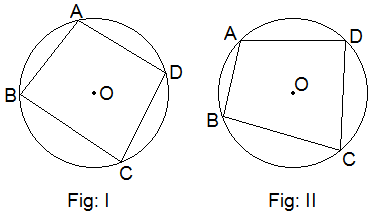
With the help of a protractor, ∠A, ∠B, ∠C and ∠D are measured and the results are tabulated below:

 

Table:

 

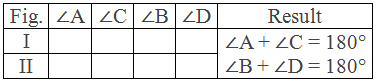
Conclusion: The above experiment shows that the opposite angles of a cyclic quadrilateral are supplementary.

 

Theoretical Proof:

 

Given: O is the centre of the circle. PQRS is a cyclic quadrilateral.

To Prove: (i) ∠P + ∠R = 180° (ii) ∠Q + ∠S = 180°

 

Proof:

Statements                       Reasons

1.  ∠P = ½ arc QRS ----> Inscribed angle is half of opposite arc.

2.  ∠R = ½ arc QPS  ----> Inscribed angle is half of opposite arc.

3.  ∠P + ∠R = ½ (arc QRS + arc QPS) -----> Adding 1 and 2.

       = ½ circle PQRS

       = ½ × 360°

       = 180°

4.  ∠Q + ∠S = 180° ------> Same as above.

Proved.