Circle Theorems on Chords

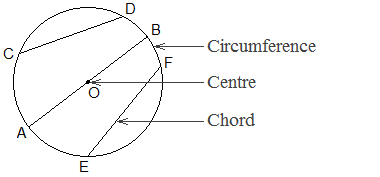
A circle is a closed plane figure bounded by a curved line at an equal distance from a fixed point. The fixed point is called the centre of the circle and the curved line is called the circumference of the circle. A chord is a line segment joining any two points on the circumference. A chord passing through the centre of a circle is called the diameter. The diameter is one of the longest chords.

 

There are certain properties of chords which are stated as the circle theorems on chords. Following are the circle theorems on chords and their proofs:

 

THEOREM 1:

“The perpendicular drawn from the centre of a circle to a chord bisects the chord.”

 

Proof:

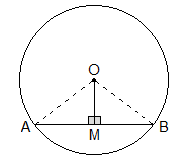
Given: O is the centre of a circle and OM is perpendicular to chord AB.

To Prove: AM = BM

Construction: OA and OB are joined.

 

Proof:

Statements                       Reasons

1.  In DAOM and DBOM

i.    ∠AMO = ∠BMO (R) ----> Both right angles; OM⊥AB

ii. OA = OB (H) -----> Radii of the same circle

iii.    OM = OM (S) -----> Common side

2.  DAOM ≅DBOM -----> By RHS axiom

3.  AM = BM ----> Corresponding sides

Proved.

 

 

CONVERSE OF THEOREM 1:

“A straight line joining the centre of circle and mid-point of a chord is perpendicular to the chord.”

 

Proof:

Given: O is the centre of a circle and OM is perpendicular to chord AB.

To Prove: OM⊥AB

Construction: OA and OB are joined.

 

Proof:

Statements                       Reasons

1.  In DAOM and DBOM

i.       OA = OB (S) ----> Both right angles; OM⊥AB

ii.    AM = BM (S) ----> Radii of the same circle

iii. OM = OM (S) ----> Common side

2.  DAOM ≅DBOM ----> By RHS axiom

3.  ∠AMO = ∠BMO ----> Corresponding angles

4.  ∠AMO + ∠BMO = 180° ----> Linear pair of angles

or, ∠AMO + ∠AMO = 180°

or, 2∠AMO = 180°

or, ∠AMO = 90°

5.  OM⊥AB ----> Being ∠AMO = 90°

Proved.

 

 

THEOREM 2:

“The perpendicular bisector of the chord of a circle passes through the centre.”

 

This theorem can be verified by an experiment. Here is the experimental verification of the theorem:

 

Construction: By using a scale, pencil and compass, three circles of different radii are drawn. Perpendicular bisectors of chords AB and CD are drawn which meet at O. In each figure O is joined with A, B, C and D.

 

Now, the measures of OA, OB, OC, and OD are tabulated below:

Table:

 

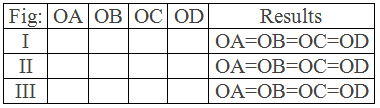
Conclusion: OA = OB = OC = OD shows that O is the centre of the circle. Hence, it is experimentally verified that the perpendicular bisector of the chord of a circle passes through the centre.

 

 

THEOREM 3:

“Equal chords of a circle are equidistant from the centre of the circle.”

 

Proof:

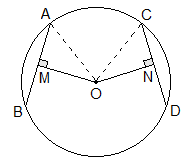
Given: O is the centre of the circle, where chord AB = chord CD. OM and ON are drawn perpendicular to AB and CD respectively.

To Prove: OM = ON

Construction: OA and OC are joined.

 

Proof:

     Statements                        Reasons

1.  AM = AB/2 and CN = CD/2 -----> Perpendicular bisect the chord.

2.  AB = CD -------> By given

3.  AM = CN -------> From statements 1 and 2

4.  In DAMO and DCNO

i.    ∠AMO = ∠CNO (R) -----> Both are right angles

ii. OA = OC (H) -----> Radii of the same circle

iii.    AM = CN (S) -----> From statement 3.

5.  DAMO ≅DCNO -----> By RHS axiom

6.  OM = ON ---------------------> Corresponding sides

Proved.

 

 

CONVERSE OF THEOREM 3:

“Chords which are equidistant from the centre of a circle are equal.”

 

Proof:

Given: O is the centre of a circle and OM is perpendicular to chord AB.

To Prove: AM = BM

Construction: OA and OB are joined.

 

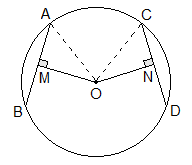
Proof:

Statements                       Reasons

1.  In DAMO and DCNO

i.    ∠AMO = ∠CNO (R) ----> Both right angles

ii. OA = OC (H) -----> Radii of same circle

iii.    OM = ON (S) -----> Given

2.  DAMO ≅DCNO -----> By RHS axiom

3.  AM = CN -----> Corresponding sides

4.  AM = AB/2 and CN = CD/2 ----> Perpendicular bisect the chord

5.  AB = CD ----> From statement 3 and 4

Proved.